One thing you should know about me is that I hate teaching using short-cut methods. When a child is being taught shortcuts, many times that becomes their primary way of doing math. This then means they are being robbed of the opportunity to really understand mathematics which results in low grades in math. Therefore, if you are someone that does not fully understand percentages, download this booklet with the title, “The theory of percentages“. This is a booklet I made that I only share with students of mine.
Read through the entire booklet, and make sure you understand everything. Once you’ve read through it, make sure you’ve answered all the questions. The questions are designed to help you reason on percentages so make sure you’ve answered them thoroughly. If you can’t answer them, do more research until you are able to come up with a sensible answer to the questions! Once you are done reading the booklet, come back to this post and keep reading.
If you do, however, understand the theory of percentages fully and you are someone who wants to learn a few shortcuts just to be quicker when calculating percentages then this post is perfect for you. To understand all the details in this post. you need to know what percentages are and how they relate to division.
First, lets discuss some of the most common percentage problems you will get and easy ways you can solve them without a calculator.
Many times, you will be given a number and you will be asked to find the percent of a number. Many of these are simple and can be solved simply using mental math.

For example, 50% of any number will be equal to half that number. So if asked what 50% of 300 is, you can simply say “150”.
25% of any number is a quarter of any number, which is half of half that number. Thus, if asked what 25% of 300 is, you can simply say “75” because half of 300 is 150 and half of that is 75.
The same principle applies to 75%. 75% is equal to 50% + 25% therefore 75% of any number is equal to half the number plus a quarter of the number. Adding those values will get you 75% of that number.
10% is a bit more interesting. You could either mentally divide the number into 10 equal pieces or parts. Lets use “10% of 200” as an example. If divide 200 into 10 equal parts, the value of each part is 20 therefore 10% of 200 is 20. And based on that, you can easily find what 20 percent of any number is, 30%, 40% etc.
Logically then, if you were asked to find the percentage of 100 out of 200, you should be able to say 50% because you know that 100 is half of 200. And if you were asked what the percentage of 50 out of 200 is, you should be able to say 25% because 50 is a quarter of 200. In essence, you should be able to use those percentage facts, or the percentage principles I just shared with you to solve even these kinds of percentage problems mentally.
But let’s talk about when the percentage isn’t ‘simple’. For example,

How can you solve that in an easy way without a calculator? Lets use this sum as an example;
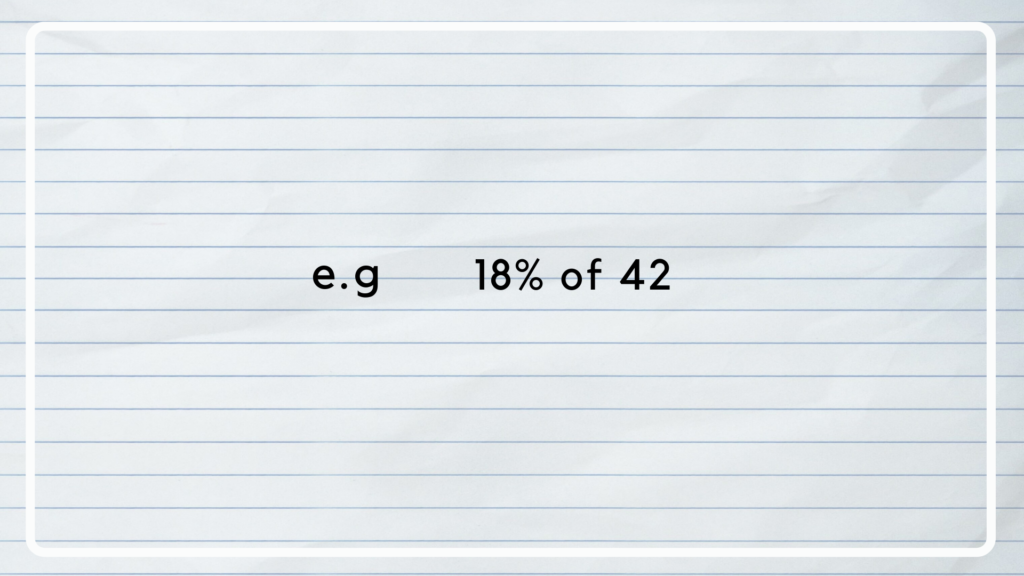
- Start off by changing the way the sum looks so it looks easier to solve.
For example, the percentage sign currently makes the sum look quite complicated, therefore you may not know what to do next. If you change the way the sum looks in a way that is mathematically correct, then your next step may be more obvious. For example,
- Change the percentage into a normal fraction. All percentages have a denominator of 100 therefore make 18% 18 over 100 Please note, you are simply changing how the sum looks! You are not changing the actual value of the sum. Our goal is to make the sum easier to solve.

- Next, change the whole number into a fraction as well. If you want to change any whole number into a fraction, the denominator is always one. Again, the value of the whole number hasn’t changed but it is now easier to solve. Also, as additional research, go find out why the denominator of every whole number is 1 when you change it into a fraction. This principle may improve your knowledge of fractions in general. You, now, have 2 fractions in front of you.

- The last change you can make is with the “of”. The general rule in mathematics is that the word “of’ in any number sentence means you must multiply. That’s the rule. Again, just as additional research, go find the principle, the why, behind that rule. Once you’ve made that change, you now have a number sentence you can work with.

2. Now, multiply the 2 fractions together to get your answer.
An easy way to do that is by multiplying the numerator with the numerator and the denominator with the denominator. I’m going to say this again; this is just another method of multiplying fractions. Do research and figure out the principle behind that method. Your understanding of fractions could improve drastically.
Once you’ve multiplied and simplified, you would’ve solved the problem in an easy and calculator-free way.

Once again, if you want an in-depth explanation of percentages, use this link to download my free booklet, “the theory of percentages”!




